[디지털 영상처리 기초] 5. 화소 단위 영상처리
1) blocks 영상 b에 대해서 다음의 명령들을 사용하라.
| b2 = imdivide(b,64); bb2 = immultiply(b2, 64); imshow(bb2) |
그 결과에 대해 간략히 설명하라. 왜 이 결과는 원 영상과 같지 않은가?
b = imread('blocks.tif');
b2 = imdivide(b,64);
bb2 = immultiply(b2, 64);
subplot(1,2,1), imshow(b), title('b')
subplot(1,2,2), imshow(bb2), title('bb2')

분명 영상의 크기는 같지만 품질이 원본 영상과 같지 않음을 볼 수 있습니다. 이유는 영상의 픽셀들을 64로 나눌 때 나머지 값들이 소실됩니다. 255를 64로 나누게 되면 0, 1, 2, 3, 4의 영역으로 나누어지게 되기 때문입니다. 이러한 소실된 데이터를 다시 64로 곱하기 때문에 원본과 다른 값을 가지게 됩니다.
2) 문제 1에서의 값 64를 32와 16으로 치환하여 수행하라. 문제 2에 있는 결과와는 어떻게 다른가?
b = imread('blocks.tif'); % blocks.tif 불러오기
b1 = imdivide(b, 64); % blocks를 각 화소를 64로 나눔
bb1 = immultiply(b1, 64); % 다시 각 화소에 64를 곱함
b2 = imdivide(b, 32); % blocks를 각 화소를 32로 나눔
bb2 = immultiply(b2, 32); % 다시 각 화소에 32를 곱함
b3 = imdivide(b, 18); % blocks를 각 화소를 18로 나눔
bb3 = immultiply(b3, 18); % 다시 각 화소에 18를 곱함
subplot(2,2,1), imshow(b), title('원본') % blocks 원본 출력
subplot(2,2,2), imshow(bb1), title('64로 만든 영상') % 64로 만든 영상 출력
subplot(2,2,3), imshow(bb2), title('32로 만든 영상') % 32로 만든 영상 출력
subplot(2,2,4), imshow(bb3), title('18로 만든 영상') % 18로 만든 영상 출력

64보다 32로 만든 영상, 32보다 16으로 만든 영상이 원본에 가깝고 영상의 품질이 좋은 것을 볼 수 있습니다. 이유는 255를 64로 나눌 때(0, 1, 2, 3, 4)보다 32로 나눌 때 영상의 영역이 더 세분화 되어있고 (0, 1, 2, 3, 4, 5, 6, 7, 8), 32보다 16으로 나눌 때 영상이 더 세분화 됩니다(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16). 따라서 영상을 나눌 때 소실되는 데이터가 적어지기 때문에 적은 수로 나눴다가 다시 그 크기만큼 곱했을 때 영상이 더 좋은 품질을 유지할 수 있습니다.
3) 카메라맨 영상을 인덱스 영상으로 변환하라.
• 원영상, 인덱스영상의 인덱스를 영상으로 디스플레이
• 위 두 영상의 히스토그램 디스플레이
• 히스토그램 스트레칭 알고리즘을 적용하여 영상을 개선하시오.
– 인덱스 영상의 히스토그램을 보고 2개의 적절한 스트레칭 함수를 만들고 디스플레이 하세요.
– 이 스트레칭 함수를 사용하여 히스토그램 스트레칭을 구현하라.
– 결과 영상과 히스토그램을 디스플레이하고 비교 설명하라.
1. 원영상, 인덱스영상의 인덱스를 영상으로 디스플레이
c = imread('cameraman.tif'); % 카메라맨 영상 불러오기
[x, map] = gray2ind(c); % 카메라맨 영상을 인덱스 영상으로 변경
subplot(1,2,1), imshow(c), title('원본') % 원영상 디스플레이
subplot(1,2,2), imshow(x), title('인덱스영상의 인덱스') % 인덱스영상의 인덱스 디스플레이

2. 위 두 영상의 히스토그램 디스플레이
subplot(1,2,1), imhist(c), axis tight, title('원본') % 원영상 히스토그램
subplot(1,2,2), imhist(x), axis tight, title('인덱스영상의 인덱스') % 인덱스영상의 인덱스 히스토그램

인덱스 영상의 인덱스는 히스토그램이 좌측(0)쪽으로 편향되어 있습니다.
3. 히스토그램 스트레칭 알고리즘을 적용하여 영상을 개선하시오.
– 인덱스 영상의 히스토그램을 보고 2개의 적절한 스트레칭 함수를 만들고 디스플레이 하세요.
– 이 스트레칭 함수를 사용하여 히스토그램 스트레칭을 구현하라.
– 결과 영상과 히스토그램을 디스플레이하고 비교 설명하라
⑴ 대비 확장 스트레칭 함수
대비 확장 스트레칭 함수를 hist1이라고 명명한 뒤 구현해봤습니다. (hist1.m으로 저장)
% 히스토그램 스크래칭(대비 확장) - Contrast 스트레칭 함수
function stretching1 = hist1(c, x)
max_c = max(c(:)); max_x = max(x(:)); % 원본의 최대 값, 참조 영상의 최대 값을 찾아줍니다.
min_c = min(c(:)); min_x = min(x(:)); % 원본의 최소 값, 참조 영상의 최소 값을 찾아줍니다.
% 스트레칭 = (d - c) / (b - a) * (i - a) + c
stretching1 = (max_c - min_c) / (max_x - min_x) * (x - min_x) + min_c
이제 hist1 함수(스트레칭 함수)를 이용해 보겠습니다.
y = hist1(c,x); % hist1 함수를 이용해서 평활화 한 값을 y에 담음
subplot(1,2,1), imhist(y), title('스트레칭 함수1'), axis tight % 스트레칭 된 히스토그램
subplot(1,2,2), imshow(y), title('스트레칭 영상1'), axis tight, figure % 스트레칭 된 영
subplot(1,2,1), imhist(x), title('인덱스영상의 인덱스'), axis tight % 인덱스영상의 인덱스 히스토그램 디스플레이
subplot(1,2,2), imhist(y), title('스트레칭 히스토그램1'), axis tight , figure% 스트레칭 된 히스토그램
subplot(1,2,1), imshow(c), title('원영상'), axis tight % 원영상 히스토그램 디스플레이
subplot(1,2,2), imshow(y), title('스트레칭 영상1'), axis tight, figure % 스트레칭 된 영상
기존 인덱스영상의 인덱스를 hist1(스트레칭 함수)를 이용해서 y에 새로 담았습니다.

스트레칭 함수 hist1을 적용한 결과입니다. 다음은 원영상과 스트레칭 된 인덱스를 비교해보겠습니다.

인덱스영상의 인덱스가 스트레칭 된 것을 확인할 수 있습니다 (위에 원영상의 히스토그램과 비슷한 모양을 가지게 되었습니다). 그렇다면 원영상과 스트레칭 된 인덱스를 비교해보겠습니다.

인덱스영상의 인덱스는 히스토그램이 좌측으로 편향되어 어둡게 나타났었는데 스트레칭 이후에 원영상과 거의 같아졌습니다. 스트레칭 함수를 적용하여 픽셀들이 좌측(0)으로 편향되어 있던 것을 전체적으로 퍼트렸기 때문에 원본 히스토그램과 유사해졌고 때문에 영상의 밝기도 다시 원래의 영상과 비슷해졌습니다. 여기서 사용된 스트레칭 함수를 확인해보겠습니다.
stretching1 = (max_c - min_c) / (max_x - min_x) * (x-min_x) + min_c
(c는 원본영상, x는 참고영상을 나타냅니다.)
이 부분이 스트레칭 함수의 핵심 부분입니다. 이 함수를 통해서 기존 영상의 범위를 원영상의 범위로 확장할 수 있었습니다. 다음은 함수를 식으로 표현한 것이며 r(감마)값은 수정하지 않기 위해 함수에는 포함하지 않았습니다.
⑵ 부분적 선형 스트레칭 함수
대비 확장 스트레칭 함수를 histpwl이라고 명명한 뒤 구현해봤습니다. (histpwl.m으로 저장)
% 대비 확장 스트레칭 함수
function out = histpwl(im,a,b)
% double이 아니면 double로 바꿈
classChanged = 0;
if ~isa(im, 'double'),
classChanged = 1;
im = im2double(im);
end
% 길이 확인
if length(a) ~= length (b)
error('Vectors A and B must be of equal size');
end
% 길이 확인
N=length(a);
out=zeros(size(im));
% 핵심 부분
for i=1:N-1
pix=find(im>=a(i) & im<a(i+1));
out(pix)=(im(pix)-a(i))*(b(i+1)-b(i))/(a(i+1)-a(i))+b(i);
end
pix=find(im==a(N));
out(pix)=b(N);
% 출력시 uint8로 변환
if classChanged==1
out = uint8(255*out);
end
이제 histpwl 함수(스트레칭 함수)를 이용해 보겠습니다.
c = imread('cameraman.tif'); % cameraman 영상을 불러옴
[x, map] = gray2ind(c); % cameraman 영상을 인덱스 영상으로 변경
new_x = histpwl(x, [0, 0.25, 0.5, 0.75, 1], [0, 0.75, 0.25, 0.5, 1]); % 스트레칭 함수 적용 후 new_x에 담음
subplot(1,3,1); imhist(c); axis tight, title("원영상 히스토그램") % 원영상 히스토그램
subplot(1,3,2); imhist(x); axis tight, title("인덱스영상 인덱스 히스토그램") % 인덱스영상 인덱스 히스토그램
subplot(1,3,3); imhist(new_x); axis tight, title("스트레칭 된 인덱스 히스토그램"), figure % 스트레칭 된 인덱스 히스토그램
subplot(1,3,1); imshow(c); axis tight, title("원영상") % 원영상
subplot(1,3,2); imshow(x); axis tight, title("인덱스영상") % 인덱스영상 인덱스
subplot(1,3,3); imshow(new_x); axis tight, title("스트레칭 된 인덱스"), figure % 스트레칭 된 인덱스
plot(x,new_x,'.'), axis tight, title("부분적 선형 스트레칭 함수")
기존 인덱스영상의 인덱스를 histpwl(스트레칭 함수)를 이용해서 new_x에 새로 담았습니다. 다음은 결과를 보겠습니다.
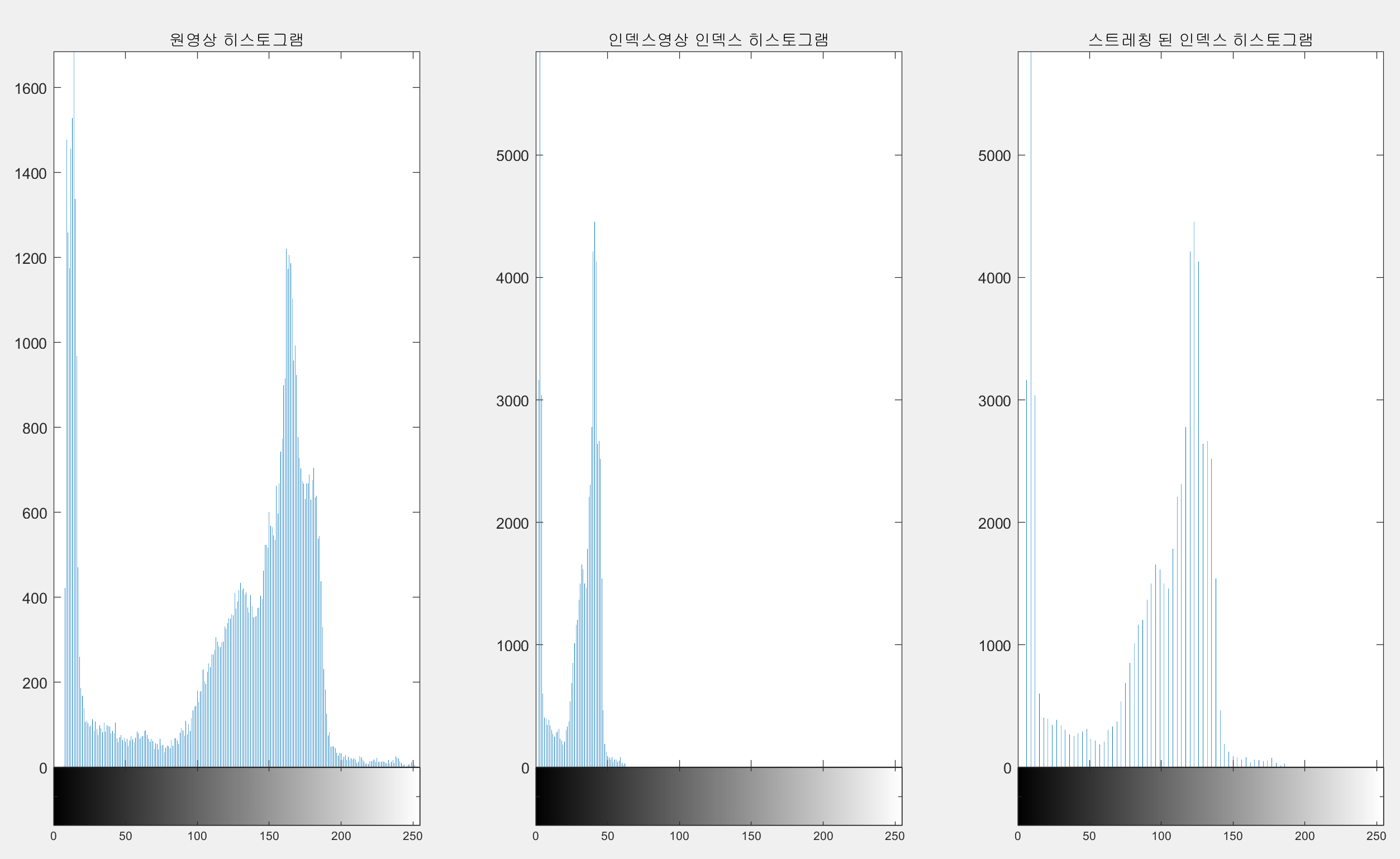

부분적 선형 스트레칭 함수를 적용한 결과 히스토그램은 원영상 히스토그램처럼 골고루 퍼지게 되었고 영상 또한 원영상과 비슷하게 나타났습니다. 인덱스영상의 인덱스 히스토그램은 좌측으로 편향되어 어두워진 영상을 출력하는 반면에 스트레칭 된 히스토그램은 밝기 값이 골고루 분포되어 영상의 원영상과 비슷하게 나오게 되었습니다. 사용된 스트레칭 함수를 살펴보겠습니다.
부분적 선형 스트레칭 함수의 핵심부분입니다.
for i=1:N-1
pix=find(im>=a(i) & im<a(i+1));
out(pix)=(im(pix)-a(i))*(b(i+1)-b(i))/(a(i+1)-a(i))+b(i);
end
a(i)와 a(i+1)사이의 값을 찾아서 out으로 보내주는데 코드의 의미는 i가 증가함에 따라서 밝기가 어두운 것부터 밝은 것까지 다음의 직선의 방정식을 만들어줍니다.

plot(x, new_x, ‘.’)을 통해서 사용한 스트레칭 함수를 디스플레이해보겠습니다.

'디지털영상처리기초 > Matlab' 카테고리의 다른 글
| [디지털 영상처리 기초] 7. Neighborhood Processing (0) | 2021.06.25 |
|---|---|
| [디지털 영상처리 기초] 6. 화소 단위 영상처리 2 (0) | 2021.06.24 |
| [디지털 영상처리 기초] 4. 영상 디스플레이 2 (0) | 2021.06.21 |
| [디지털 영상처리 기초] 3. 영상 디스플레이 (0) | 2021.06.20 |
| [디지털 영상처리 기초] 2. 영상과 매트랩 (0) | 2021.06.19 |




댓글